地頭力を鍛える(フェルミ推定)
地頭力を鍛える一番良い方法はフェルミ推定であると言われています。
『フェルミ推定(フェルミすいてい、英: Fermi estimate)とは、実際に調査するのが難しいようなとらえどころのない量を、いくつかの手掛かりを元に論理的に推論し、短時間で概算することを指す。オーダーエスティメーションや「封筒裏の計算(英語)」ともいわれる。』
フェルミ推定はコンサルの面接や外資の面接などで良く問われることがあります。
何故、面接で問われると思いますか?
それはフェルミ推定は暗記では対応できないと考えられており、答えのない問に対して仮説を立て論理的に考えることが求められる為、求職者のふるい落としを効率的に行えるからなのです。効率的にとはそれだけ明暗がわかれる問いであり、普段から頭を使っている人と使っていない人の差がとても明確になります。
そんなフェルミ推定ですが、今回は体系立てて少しでもフェルミ推定を理解し、知の世界に足を踏み入れてほしいと考え書いております。
(0)学ぶ前に知っておくと良いこと「ストック問題」と「フロー問題」
ストック、フローとは?
まず、フェルミ推定問題を大きく二分する「ストック」(stock)と「フロー」(flow)という用語について説明します
辞書で「ストック」を調べると「ある一時点に存在する経済諸量の大きさを示す概念」、一方で「フロー」は「経済諸量が一定期間内に変化または生起した大きさを示す概念」という説明が出てきます。
よりかみ砕いて説明するならば、「ストック」とは「あるモノの一時点における存在量」のことであり、一方で「フロー」は「あるモノの一定期間における変化量」のことです。
たとえば、「ピアノ」を例に考えてみましょう 。
○ストックとフローの具体例
「シカゴにおけるピアノの数」と「シカゴにおけるピアノの市場規模(年間)」……果たしてどちらが「ストック」で、どちらが「フロー」でしょう
答えは、「シカゴにおけるピアノの数」が「ストック」であり、「シカゴにおけるピアノの市場規模(年間)」が「フロー」です。
市場規模(年間)は1年間のピアノのシカゴ内総販売額を集計したものですから、「1年間という一定期間で自動車がシカゴで売られた量(金額)」といえますね
たとえていうと、「ストック」は「容器の中の水の量」であり、「フロー」は「一定時間に蛇口から容器へ注がれる(容器から出ていく)水の量」です。後者の「フロー」は、「1分間に10リットル」のように、一定時間あたりの量を表しているという特徴があります。
(1)基本ステップの解説
フェルミ推定は、基本的に次の5つのステップで進めていきます。
①前提確認 ②アプローチ設定 ③モデル化 ④計算実行 ⑤検証
ここでは、一番有名で基本である「シカゴにピアノの調律師は何人いるのか。」という問題を例に、この5つのステップを順に説明していきます。
①前提確認
ここでは「ピアノ」の定義を明確にしていきます。今回で言うと調律できるピアノであり、電子的なピアノは含まれていません。※今回は家庭にあるピアノを算出していきます。
ⅰ.「ピアノ」をどのように定義をするか「定義」
ⅱ.どのような「ピアノ」を数えるのか「範囲の限定」
を明確にしていきます。
②アプローチ設定
ここでは基本的な式を設定します。いきなりシカゴのピアノの調律師の数を導き出すことはできません。
そこで中学校でならった因数分解をしていきます。
シカゴのピアノの調律師の数を出すためには、
ピアノ調律師の数=ピアノ調律需要÷調律師一人当たりの年間調律件数
を導き出すと答えにたどり着きます。
ここで前提となっている認識としては、需要=供給 ということです。
需要というのはピアノの調律師です。「シカゴでいったいどのくらいのピアノの調律需要があるのか?」という数字です。
供給量というのは、まさにピアノ調律師の数です。シカゴにはその地域のピアノ調律需要を満たすに十分な調律師がいるはずだと考えよということです。
③モデル化
ここでは②アプローチ設定で立てた基本式の深堀を行っていきます。
基本式をみていくと、『ピアノ調律需要』『調律師一人当たりの年間調律件数』という変数があります。
この2つの変数をさらに因数分解していくことを③モデル化で行っていきます。
②アプローチ設定と③モデル化の違いは前者は横のアプローチであり、後者は縦のアプローチとなっています。
ピアノ調律需要=シカゴ世帯数×ピアノ保有率×ピアノ調律の頻度
調律師一人当たりの年間調律件数=一日あたり調律件数×年間労働日数
に因数分解をすることができます。
④計算実行
それでは③で求めたモデル式を計算していきます。
ピアノ調律需要=シカゴ世帯数×ピアノ保有率×ピアノ調律の頻度
▼世帯数の推定
シカゴ世帯数はどう求めるかというと、人口÷平均世帯人数です。
シカゴの人口はどうやって求めるの?そんなの知らないよ!と思われるかもしれないですが、ここで大切なことは推定のためにどういう推定式を使うか、という論理の方です。実際は③モデル化までは導き出せればほぼフェルミ推定は完了しています。
ここではざっくり東京の人口が1000万人だからそこまではいかないだろう。でも都市としては世界で10番目ぐらいには入っていそうだ。なので300万人ぐらいと予想しよう!
みたいな感じで最初の方は考えて問題ありません。フェルミ推定を嫌いになるぐらいならそれぐらいの気軽さで考えたほうが良いと思っています。
考え方というのは習慣にしないと確実に身に付きません。ですので、まずはやってみることが大切なのです。
次に平均の世帯数ですが、感覚的に母親、父親、子供が平均的な世帯であると仮定し、
3人とします。結果としてシカゴ世帯数は300万人÷3人=100万世帯と導ぎだせます。
▼ピアノ保有率の推定
シカゴ世帯数が100万世帯としたときに、ピアノを保有する可能性があるとする裕福なファミリー層は50%といると仮定し、そして実際に保有する世帯を10%で計算していきます。
100万世帯×50%×10%=5万台
シカゴの家庭で保有されているピアノの数は5万台という結論が出ました。
そしたピアノ調律頻度はざっくり年一回程度だろうと仮定します。
そうすると、
ピアノ調律需要
=シカゴ世帯数×ピアノ保有率×ピアノ調律の頻度
=100万世帯×5%×1回/年間
=5万件/年間
と導くことができます。
調律師一人当たりの年間調律件数=一日あたり調律件数×年間労働日数
▼一日あたり調律件数
こちらはピアノの調律は各家庭を回るわけですから、移動時間等のコストが入ります。
そう考えると、大体午前1回、午後2回程度の調律が想定できます。
ですので一日あたりの調律件数を3件と仮定します。
▼年間労働日数
こちらざっくり土日を休みにして大体200日ぐらいだろうと仮定します。
そうすると、
調律師一人当たりの年間調律件数
=一日あたり調律件数×年間労働日数
=3件×200日
=600件
と求めることができます。
そして最後に上記で求めた変数を代入すると、
ピアノ調律師の数=ピアノ調律需要÷調律師一人当たりの年間調律件数
=5万件/年÷600件/年
=約83人
と導くことができました。
ここで気を付けてほしいことは「単位を揃えるということ」です。
今回の問題で言えば「年間」で統一をしています。
⑤検証
検証の方法として一番簡単なのが、
シカゴの人口で割ってみるということです。
300万人÷83人=36,000人
約36,000人に1人の割合でピアノ調律師が存在することになります。
30人に1人とかの割合で出してしまうと公務員ぐらいの数になってしまうので、
明らかにどこかの推論が間違っている可能性があります。
ですので今回の推論をおそらくこのぐらいの数であろうということが分かります。
すぐに読めるのでお勧めです↓
ジャンガおじさん統計学を学ぶ。その5(ビジネス応用編)
こんにちは、ジャンガおじさんです。
前回はかなりザクっと確率分布についてまとめていきましたので、
今回記事の中で出てきた分布について具体的に掘り下げていきます。
下記のケースを読んでみてください。
あなたWEBサービスの責任者です。
・あなたが働いている企業では3か月前に検索サービスをリリースしました。
・検索サービスは広告モデルで広告収入を得て成り立っています。
バックオフィスのエンジニアが駆け寄ってきてこんなことを言ってきました。
「新しいUIはサーバーへの負荷が高いので1分間に同時に980人検索サイトに訪れるとかなり読み込みが遅くなり重たくなってしまいます。1000人を超えるとアウトです。。。。」
下のデータは12月5日の1分間ごとの来訪者数です。
この時の検索サービスの1分間の平均来訪者数を940人だとします。
| 時間 | 分 | 来訪者 |
| 0 | 0 | 776 |
| 0 | 1 | 886 |
| 0 | 2 | 989 |
| 0 | 3 | 835 |
| 0 | 4 | 760 |
| 0 | 5 | 875 |
| 0 | 6 | 769 |
| 0 | 7 | 865 |
| 0 | 8 | 962 |
| 0 | 9 | 827 |
| 0 | 10 | 813 |
| 0 | 11 | 916 |
| 0 | 12 | 944 |
| 0 | 13 | 967 |
| 0 | 14 | 878 |
| 0 | 15 | 885 |
さて、1001人以上の人が同時に検索サービスに来訪する確率はどの程度でしょうか???
ある程度イメージはできているでしょうか。
統計学を用いると将来をある程度予測することができるので、
不確実性が高いビジネス世界においてとても重宝される学問であり、
ビジネスとはとても相性が良いのです。
では、具体的に考えていきましょう。
まずやることは
1、まずサンプルデータの形を確認する
ヒストグラムを作ると、1001人以上の同時にサイトに訪れてはいないことがわかります。
では、1001人以上の同時来訪はない=確率0%なのでしょうか??
いいえ、違うのです。


λ(ラムダ)というのは平均を表しています。
ポアソン分布で言うパラメーターとは平均のことであり、
つまり平均が分かれば分布の形を特定することができるのです。
では平均はどこから持ってくればよいのでしょうか?
それは、、、

| イベント数(=k) | 0人から1000人までが起動するので | 1000 |
| 平均(=λ) | 検索サイトを1分間に訪れる平均人数 | 940 |
エクセルで解き方を考えてみましょう。
今回の場合は、
1分間で1001回以上の来訪が発生する確率ですので、
1- (1分間で1000回以下来訪する確率)
になります。
ポアソン分布のエクセル関数は、
POISSON.DIST(イベント数,平均,関数形式)
ですので、エクセルの式はこうなります。
=1-POISSON.DIST(1000,940,TRUE)
=2.51%
よって、1001人以上の人が同時に検索サービスに来訪する確率は2.51%
この2.51%を許容するのか、しないのかはビジネスジャッジになります。
ただ、サーバーおちるのかなーおちないのかなーでも危なそうだようなー
みたいな感覚的に仕事を行うよりも、2.51%という数字を用いて議論するのとでは
全然違います。より経営判断がしやすくなり、データドリブンで仕事ができるようになるのです。
博多行ったら絶対行ってほしい店
どうも、ジャンガおじさんです。
昔仕事の関係でしばらく博多に滞在していて、今回は博多に行ったら必ず行ってほしいお店をご紹介いたします。
(個人的に博多ラーメンは外します。昔食べ過ぎて今では豚骨の匂いを嗅いだだけで気持ち悪くなってしまいますので。)
まず、最初におススメするのが『水たき 長野』。
福岡といえば水炊きなんすよね。福岡行くまでは全然知らなくて、行って現地の人に教えてもらいました。めちゃくちゃ人気なので予約1か月ぐらい普通にかかっちゃいます。残念なところとしてはクレジットカードが使えないんですよね。さっさっと導入してほしいです。
次におススメするのが『はじめの一歩』

ここ来たら、黙ってゴマサバ、ゴマカンパチを喰うべし。
ここまでのクオリティのゴマサバはなかなか東京じゃ味わえないです。
海鮮系なら一番おススメのお店です。
そして、個人的に一番おススメするのがこちらです。
『博多とりかわ大臣』

個人的に一番好きです。
もちろん一番おススメなのがとりかわです。
あの串に刺さったカリカリのとりかわを食べたときは衝撃を受けました。
もつ鍋に関しても美味しいお店たくさんありますが、
ぶっちゃけ東京にも同じような店はたくさんあります。(六本木とか)
水炊きなら『長野』
ゴマサバなら『はじめの一歩』
とりかわなら『とりかわ大臣』(とりかわ粋恭のとりかわもうまいです。)
是非、一度足を運んでみてください。
ジャンガおじさん統計学を学ぶ。その4(確率分布編)
正規分布とは、平均を μ ・分散を σ2 とした場合に以下の確率密度関数で表される確率分布を指し、N(μ, σ2)と表記されます。
また、ある確率変数X の確率分布が正規分布N(μ, σ2)であるとき「確率変数 X はN(μ, σ2)に従う」と言い、『X ~ N(μ, σ2)』と表記されます。

ビジネスで正規分布が当てはまるケース





ジャンガおじさん統計学を学ぶ。その3(確率分布編)
こんにちは、ジャンガおじさんです。
前回は平均、標準偏差など基礎中の基礎についてまとめていきました。
今回はいよいよ統計学っぽいことを学んでいきます。
今回学ぶことは『確率分布』についてです。
聞いたことはありますでしょうか。
世の中で一番有名な確率分布は正規分布であると思うのですが、
確率分布は正規分布だけではないのです。
今回は確率分布についてしっかり学んでいきましょう。

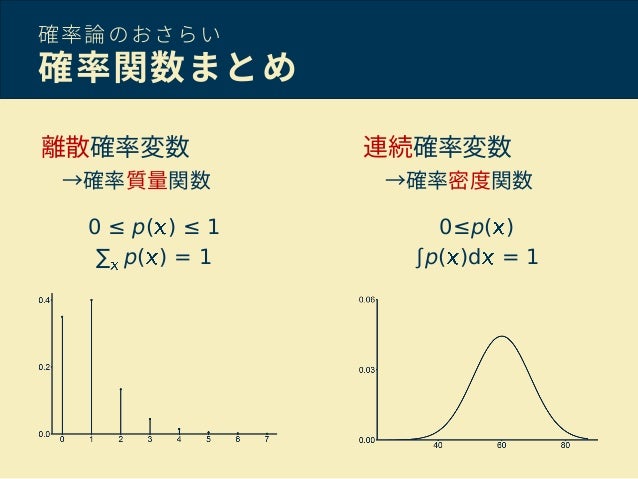
図1
ジャンガおじさん統計学を学ぶ。その2
こんにちは、ジャンガおじさんです。
前回に引き続き統計学を学んでいきました。
| N=6 | 使用意向平均点数 |
| サービスA | 3点 |
| サービスB | 3点 |
| 満足度 | ||
| 顧客ID | サービスA | サービスB |
| 1 | 3 | 1 |
| 2 | 3 | 5 |
| 3 | 3 | 1 |
| 4 | 3 | 5 |
| 5 | 3 | 1 |
| 6 | 3 | 5 |


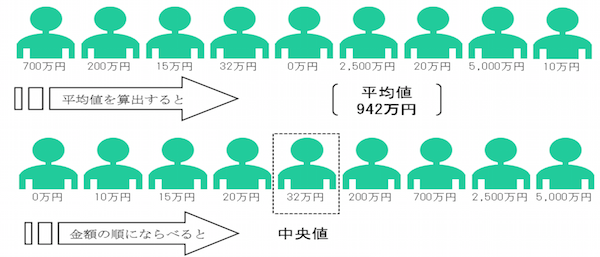
| 平均 | 中央値 | |
| サンプル数 | 多い | 少ない |
| データの分布 | 左右対称 | 左右対称ではない、外れ値がある |
これだけ覚えておけば問題ありません。

